欢迎您注册蒲公英
您需要 登录 才可以下载或查看,没有帐号?立即注册
x
本帖最后由 3048414868 于 2023-9-26 16:04 编辑
在数据分析过程中,往往需要数据服从正态分布,正态分布,也称“常态分布”,又名高斯分布,在求二项分布的渐近公式中得到。很多方法都需要数据满足正态分布,比如方差分析、独立t检验、线性回归分析(因变量)等。如果说没有这个前提可能会导致分析不严谨等等。所以进行数据正态性检验很重要。那么如何进行正态性检验?接下来进行说明。 一、检验方法一般常用的三种正态性检验的方法,分别是描述法、正态性检验以及图示法,其中图示法包括直方图以及P-P/Q-Q图。
1.描述法
理论上讲,标准正态分布偏度和峰度均为0,但现实中数据无法满足标准正态分布,因而如果峰度绝对值小于10并且偏度绝对值小于3,则说明数据虽然不是绝对正态,但基本可接受为正态分布。从上表可以看出例子中峰度为1.160绝对值小于10,偏度为-1.084绝对值小于3。说明数据基本可以接受为正态分布。 2.正态性检验SPSSAU的正态性检验包括三种:正态性shapro-WiIk检验、正态性Kolmogorov-Smirnov检验和Jarque-Bera检验。
背景简单描述:调查一个班级的53名学生的身高,判断搜集的数据是否满足μ=140.79,σ=8.6的正态分布。
由于n>50,所以检验方法选择K-S检验或者J-B检验。如果利用K-S检验进行证明,步骤如下:
1、假设检验
H0:x服从μ=140.79,σ=8.6的正态分布
H1:x不服从μ=140.79,σ=8.6的正态分布
附表如下:
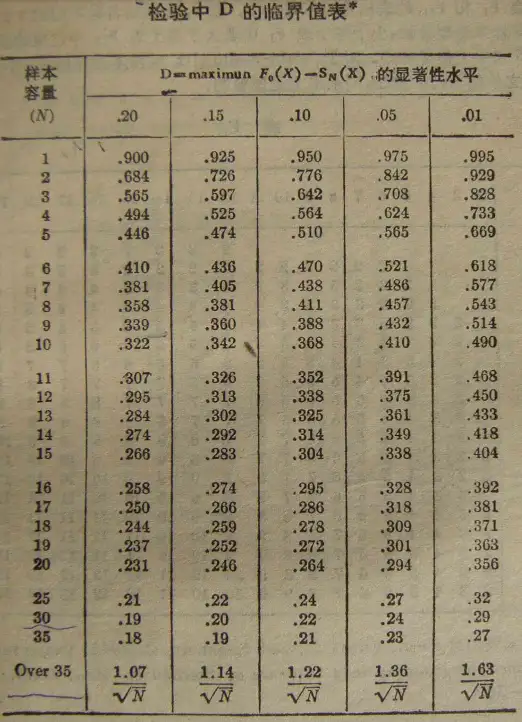
因为样本超过35,并且α=0.05,所以D53,0.05约为1.36/≈0.187; 首先计算K-S检验中的D统计量,计算公式如下: 先将数据按从小到大进行排序,用x(k)进行描述,k代表次序,然后计算其标准化的数据,标准化公式为: 接着算出每个数据的频次,并记录好累积频次,然后计算Fn(x(k)),(N为累积频次),n为样本量即例子中的53。 F0(x(k))为给定的累计分布可以利用excel自行算出,函数为:‘=NORM.DIST(x,mean,sd,TRUE) mean和sd就为u和sigma,进而可以求出和;各个步骤的计算如下:
所以可以算出D为0.218,D大于0.187,所以拒绝原假设,接受备择假设所以不满足。同时可以使用SPSSAU进行检验更为方便,数据格式如下:
分析结果如下:
从上述结果得到,样本量大于50,所以选择K-S检验,发现统计量D为0.218(和计算的一样),p值小于0.05,所以模型显著,拒绝原假设,数据不服从正态分布。 同时还包括JB检验:
Jarque-Bera检验中,p值小于0.05,所以模型显著,拒绝原假设,数据不服从正态分布(针对SPSSAU提供统计量为卡方值的原因:有证明显示在正态性假定下,JB统计量渐近地服从自由度为2的卡方分布)。 3.图示法(1)直方图
直方图若呈现‘中间高,两边低,左右基本对称的钟形图’则基本服从正态分析,但是数据量过少等也可能影响结果导致很难呈现出标准的正态分布,如果是这种情况如果看见‘钟形’也可以可以接受的。上图可以看出,数据呈现的分布并不对称,但是也出现近似‘钟形’曲线,所以也可以勉强接受。 (2)P-P图
P-P图是将观察累积概率作为X轴,将正态累积概率作为Y轴,作散点图,反映实际累积概率与理论累积概率的符合程度。如果散点分布近似‘对角线’则可以认为正态分布,从图中可以看出数据散点分布不是很满足要求,但是也近似为‘对角线’所以勉强接受。 (3)Q-Q图
Q-Q图和P-P图功能一致,分析上大致没有区别。 二、如何进行正态性检验SPSSAU分析位置(1)通用方法板块 SPSSAU【通用方法】→描述/ SPSSAU【通用方法】→正态性检验;
(2)可视化板块 SPSSAU【可视化】→直方图/ SPSSAU【可视化】→p-p/q-q图;
三、非正态数据怎么办
针对上述几种方法,正态性检验最为严谨,但是实际数据由于样本量较少等原因,即使数据总体正态但统计检验出来也显示非正态,实用性没有图示法直观且接受性没有图示法高,所以在分析中常常图示法应用的比较多,如果在分析中数据严重不正态应该怎么办呢?接下来进行说明。 (1)将数据取对数处理 注意:原数据需要数据大于0,如果不满足也可以取lg(x+k)等。 (2)开根号 (3)取倒数 当数据波动较大时可以优先考虑. (4)Johnson转换 (4) 计量经济学中常用的BOX-COX变换 (5)移除可能异常值 通常情况下,数据经过处理会变得相对“正态”一些;此步可使用SPSSAU的“生成变量”功能即可完成。或者严重不符合正态分布无法进行分析也可以使用其他分析方法,比如非参数检验等。
|  |手机版|蒲公英|ouryao|蒲公英
( 京ICP备14042168号-1 ) 增值电信业务经营许可证编号:京B2-20243455 互联网药品信息服务资格证书编号:(京)-非经营性-2024-0033
|手机版|蒲公英|ouryao|蒲公英
( 京ICP备14042168号-1 ) 增值电信业务经营许可证编号:京B2-20243455 互联网药品信息服务资格证书编号:(京)-非经营性-2024-0033